In this installment of “Writer Fuel” I show my true colors in all their geeky glory. Warning: things are going to get a bit nerdy up in here. Just saying.
As with previous installments, this topic first came up in the DIY MFA newsletter. If you’re already an email subscriber, you can help me choose letters that get featured here by replying to the emails you loved most. If you’re not on the list, but want a sneak peek at this column before it hits the blog (and want to help crowd-source it too), go here to sign up.
Dear word nerd,
Most people think of math a logical, straightforward subject. There are right answers and wrong answers, and in between them there’s little wiggle room for any shades of grey. At least, that’s what I thought, at first. Everything changed in ninth grade geometry.
Picture this scene if you will. It’s 1992 just before the holidays, and my geometry class has finished the lessons in that particular unit. Our teacher Mr. W has two options (A) start new material even though we’ll be leaving for winter break in two days and will likely forget it all, or (B) find some way to keep a classroom of adolescent prep-school girls from devolving into utter chaos. Using the teacher equivalent of a Jedi mind-trick, Mr. W comes up with secret option C. He decides to teach us some non-Euclidean geometry. You know, just for kicks. I’m sure you can imagine the collective groan that ensued.
And yet there was something kind of cool about learning math where none of the expected rules applied. Maybe I’m just the biggest dork of all time but I learned more about education and life in those two days of non-Euclidean geometry than I did in most of high school, college, and beyond.
First: A Quick Math Lesson
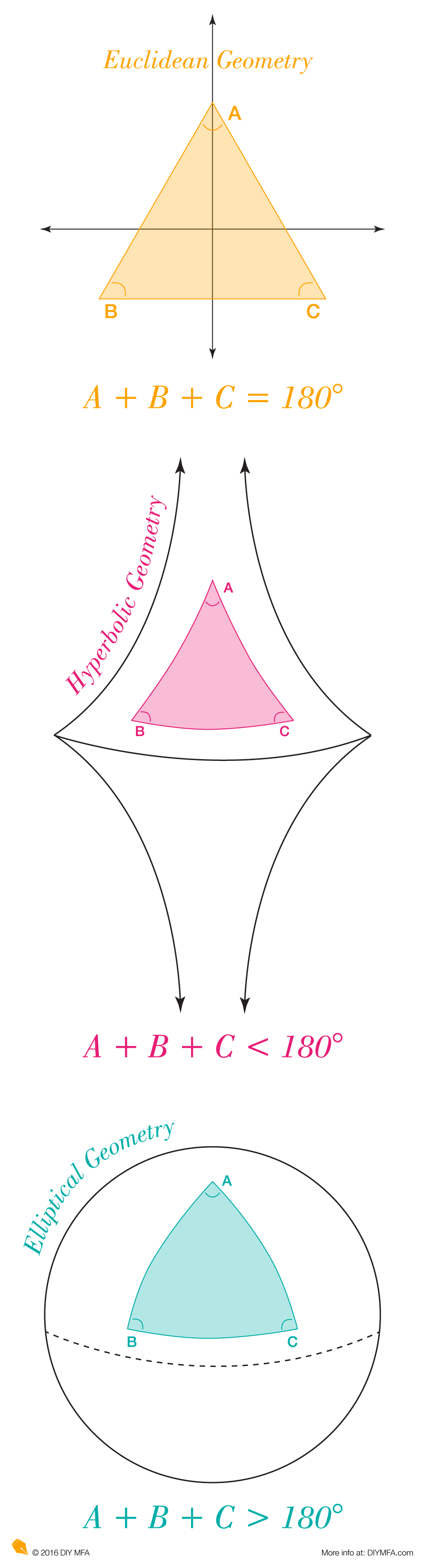 Most geometry we learn at school takes place on a flat plane. In this Euclidean world, we can count on certain rules to apply. For instance, the angles in a triangle always add up to 180 degrees. This rule—along with all the other ones we learn in Euclidean geometry—is irrefutable and there are mathematical ways to prove it.
Most geometry we learn at school takes place on a flat plane. In this Euclidean world, we can count on certain rules to apply. For instance, the angles in a triangle always add up to 180 degrees. This rule—along with all the other ones we learn in Euclidean geometry—is irrefutable and there are mathematical ways to prove it.
And yet…
When we put that same triangle on a different plane—an elliptical plane (i.e. a ball) or a hyperbolic plane (shaped like two trumpets kissing)—then all of a sudden the geometric rules change. Remember how the angles of the triangle added up to 180 degrees? That’s no longer true.
Because an elliptical plane is convex, the sum of the angles in a triangle are actually a little bit greater than 180 degrees. Conversely, because a hyperbolic plane is concave, the sum of the angles will be slightly smaller than 180 degrees.
This same logic doesn’t just hold true for triangles. Many of those rules that we take for granted in Euclidean geometry no longer apply when you explore them in either hyperbolic or elliptical space. For a picture of what I mean, take a look at the infographic on the right.
But you’re probably wondering what all this has to do with writing.
Guess What! There Are No Rules
Even in a subject like math, where we might expect rules to be absolute, it turns out that “rules” are relative and often based on context. As writers, we grapple this tension between rules and context all the time. Yet, as humans we often take rules at face value. We accept certain “rules” as facts, without stopping to consider how the context—the space where those rules operate—might shape or affect them.
As a ninth grade geometry student, I accepted that the sum of the angles in a triangle equaled 180 degrees. This was fact. It was GOSPEL. Then Mr. W starts spouting heresy, telling us that if we put that very same triangle in a different space, the rules would suddenly change.
This lesson taught me something much bigger than just the sum of the angles in a triangle. I learned that “rules” aren’t really rules, but they depend entirely on the context where they exist. In that moment, I realized that there is more than just one way to challenge rules and question authority.
Until then I had always thought that the only way to be a rebel—the only way to stand up to authority and question the status quo—was by breaking the rules. This iconoclastic approach never sat well with me because I don’t enjoy drama and I dislike hurting people.
Suddenly I saw a different way to be a rebel. If I didn’t like a particular rule, I didn’t have to break it in order to get the answer I wanted; I just had to change the context. If I could take a regular old triangle and make those angles add up however I wanted just by putting it on a different plane, I could do the same with any rule—mathematic or otherwise.
Change the Rules By Changing the Context
You could say that this was the moment when my inner-instigator was born and this change-the-context mindset is something I’ve carried with me ever since. DIY MFA is, after all, a perfect example of how you challenge rules simply by changing their context. My goal with this program has never been to fight against the traditional MFA. In fact, I’ve often talked about how I find the MFA-vs.-Not-MFA debate a bit ridiculous.
When I created DIY MFA, I wanted to offer writers an alternative context, a different “education sandbox” to play in, as it were. After all no two people are alike, so it’s silly to think that the same methods of learning and teaching would work for everyone. Some kids enjoy the swings and others prefer the slide. I myself was the weird loner, looking for volcanic rocks and digging for buried treasure. The beautiful thing about writing, though, is that we can all pursue it in our own way, and the literary playground is plenty big enough for everyone.
So go on out there, change the context, and challenge the rules.
Until next time, keep writing and keep being awesome!








